The Gorr Specification Language
version 0 by Kyle Williams - June 2nd, 2023
Gorr (a sorry pun on al-gor-ithm) is a formal natural specification language. It is meant to guide software development, allowing one to focus on defining behavior instead of implementation. In contrast to previous formal specification languages, Gorr’s syntax is entirely rooted in English; this is done in the hopes that specifications written in Gorr can be parsed by those with little or no specification experience.
What follows this introductory section is a description of the language’s features alongside a grammar written in Extended Backus-Naur Form (EBNF) and two example specifications.
To understand this document, it is recommended that one have some familiarity with arithmetic and computer programming.
A grammar written in EBNF consists of a series of rules. Each rule’s job is to scan a piece of text for a defined pattern, which itself is a sequence of symbols. A piece of text is valid according to the grammar if the text can be matched by the pattern of the top-level rule of the grammar.
⟨rule name⟩ → ⟨pattern of rule⟩;
The base symbol of EBNF is the string, which represents matching the series of characters in between a string’s pair of quotes.
“ban” matches the text “ban” but not “bat” or “banner”.
There are two special character sequences that can show up in a string to represent matching a character that normally can’t be seen: “\t” matches the tab (“ ”) and “\n” matches the beginning of a new line.
Multiple symbols can be referenced in one pattern putting a space between each symbol; note that the space does not become part of the rule. Rules can be referenced in other rules by writing the name of the rule between two angle brackets (⟨ ⟩).
⟨ban⟩ → “ban”;
⟨banner⟩ → ⟨ban⟩ “ner”;
⟨banner⟩ matches “banner” but not “ban” or “ban ner”.
Multiple symbols can be combined into one symbol by encasing them in parentheses (( )). The following two rules are equivalent:
⟨hello⟩ → “hello” “world”;
⟨hello⟩ → (“hello” “world”);
The matching behavior of symbols can be modified with operators. The union operator, marked by the pipe (|), can be used to say the matching of two or more patterns is valid.
⟨digit⟩ → “0” | “1” | “2” | “3” | “4” | “5” | “6” | “7” | “8” | “9”;
⟨digit⟩ matches “0”, “5”, and “9”, but not “a” or “9ban” or “99”.
The optional operator, marked by the question mark (?), is equivalent to creating a union between a symbol or an empty string (“”). The following two rules are equivalent:
⟨goodbye⟩ → “goodbye” “world”?;
⟨goodbye⟩ → “goodbye” (“world” | “”);
The one or more operator, marked by the plus (+), enables a symbol can be matched one or more times.
⟨aaaaah⟩ → “a”+ “h”;
⟨aaaaah⟩ matches “ah”, “aaaaaaaaaaaaaaaah”, and “aaaaah”.
The zero or more operator, marked by the asterisk (*), is equivalent to combining the one or more and optional operators. The following two rules are equivalent:
⟨inputs⟩ → (“a” | “b” | “x” | “y”)*;
⟨inputs⟩ → ((“a” | “b” | “x” | “y”)+)?;
There is one more kind of symbol: a special sequence, arbitrary text enclosed between two question marks (? ?), can be used to define a pattern that would be challenging to describe in EBNF.
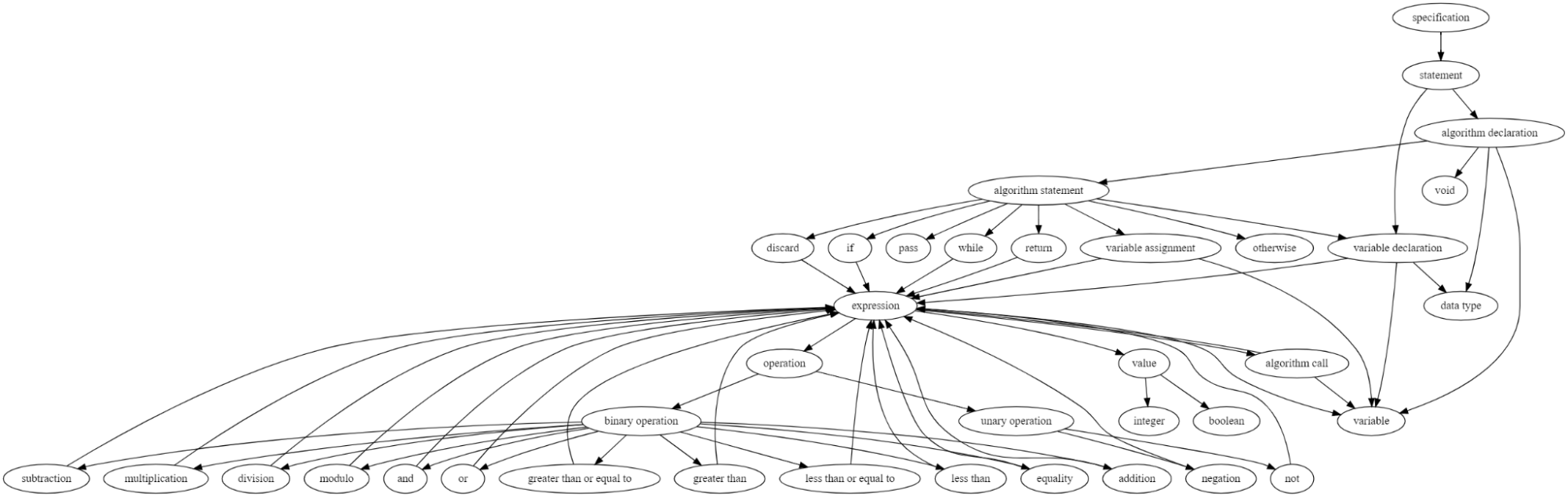
The above map is a dependency graph of concepts in the Gorr language created from its grammar. Concepts point towards other concepts they rely on. Some dependencies are cyclical; for example, binary operators are a kind of expression, but they themselves rely on the existence of expressions, otherwise, you wouldn’t be able to nest operations and other expressions inside of them.
In order for a Gorr specification to be valid, it must follow the EBNF grammar described in the latter sections of this description.
⟨space⟩ → (“ “ | “\t”)+;
⟨newline⟩ → “\n”;
⟨period⟩ → “.”;
⟨comma⟩ → “,”
⟨digit⟩ → “0” | “1” | “2” | “3” | “4” | “5” | “6” | “7” | “8” | “9”;
⟨integer⟩ → “-”? ⟨digit⟩+;
⟨boolean⟩ → “true” | “false”;
⟨value⟩ → ⟨integer⟩ | ⟨boolean⟩;
⟨data type⟩ → “integer” | “Boolean”;
Gorr has two standard data types[1]: the integer and the Boolean. Data types can be manipulated by operators.
⟨specification⟩ → ⟨statement⟩+;
⟨statement⟩ → (⟨variable declaration⟩ | ⟨algorithm declaration⟩) ⟨newline⟩;
A specification written in Gorr is a series of statements, either variable or algorithm declarations.
⟨variable⟩ → “[[” ⟨space⟩? ⟨text⟩ ⟨space⟩? “]]”;
⟨variable declaration⟩ → “The” ⟨space⟩ ⟨data type⟩ ⟨space⟩ ⟨variable⟩ ⟨space⟩ “is” ⟨expression⟩ ⟨period⟩;
⟨variable assignment⟩ → “Set” ⟨space⟩ ⟨variable⟩ ⟨space⟩ “to” ⟨space⟩ ⟨expression⟩ ⟨period⟩;
Variables in Gorr can be used to store and retrieve values. The value of a variable can be changed with an assignment.
When declaring a variable, one must give it a name, a type, and an initial expression that evaluates to a value of that.
When assigning a value to a variable, the expression given must match the type of the variable.
Variables declared at the top of a specification are constants, and cannot be modified with an assignment after declaration.
When a variable is declared, it enters scope, and a variable with the same name cannot be declared again until it exits scope. A variable exits scope when:
Constants never exit scope.
Variables cannot be referenced in assignments or expressions before they enter scope.
⟨algorithm declaration⟩ → “The algorithm” ⟨space⟩ ⟨variable⟩ ⟨space⟩ ⟨comma⟩
(* Arguments*)
“with the signature” ( ⟨data type⟩ ⟨space⟩ ⟨variable⟩ (⟨comma⟩ ⟨space⟩ ⟨data type⟩ ⟨space⟩ ⟨variable⟩)*)? “returns” (⟨data type⟩ | “void”) ⟨comma⟩
“does the following:” ⟨newline⟩
(* Body *)
(<space>? ⟨digit⟩+ (⟨period⟩ ⟨digit⟩)* ⟨period⟩ ⟨space⟩ ⟨algorithm statement⟩ ⟨newline⟩)+;
⟨algorithm statement⟩ → ⟨if⟩ | ⟨otherwise⟩ | ⟨while⟩ | ⟨return⟩ | ⟨variable declaration⟩ | ⟨variable assignment⟩ | ⟨discard⟩ | ⟨pass⟩;
Algorithms are the core unit of Gorr; they are used to specify and encapsulate chunks of logic. An algorithm has a name, an optional series of arguments with specified types, a return type, and a series of numbered statements.
The values of expressions passed to an algorithm as arguments must match each argument’s type.
Algorithms have the same scope behavior as constants; an algorithm can be called inside of itself to implement recursive algorithms.
Arguments have the same scope behaviors as regular variables; as such, two arguments cannot have the same name.
⟨discard⟩ → “Discard” ⟨space⟩ ⟨expression⟩ ⟨period⟩;
Algorithms have one special data type that can be used only as the return type: void. A void value has no value literal. A void value can be generated by an empty return statement inside an algorithm with a void return type, or a void algorithm.
The value of an expression can be thrown away with a discard statement. This is most useful for calling void algorithms, as nothing can be done with void values otherwise.
Void algorithms are useful for specifying side effects, such as printing to standard output.
Control flow can modify the execution order of statements in algorithms depending on the value of expressions. A series of statements inside of a control flow statement is known as a block. When inside a block, you must indent all statements inside that block. For example:
1. If true, // zero levels of indentation
1.1. While true, // one level of indentation
1.1.1. Return. // two levels of indentation
2. Otherwise, // zero levels of indentation
2.1 Pass. // two levels of indentation
⟨if⟩ → “If” ⟨space⟩ ⟨expression⟩ ⟨comma⟩;
⟨otherwise⟩ → “Otherwise” ⟨comma⟩;
If the expression of an if statement, known as its condition, evaluates to true, the if block and only the if block is executed. Otherwise, the block of the otherwise statement is executed. This is useful for representing branches in logic.
An otherwise statement must come immediately after an if statement.
⟨pass⟩ → “Pass” ⟨period⟩;
This statement does nothing. Use it when you only care about only the if or otherwise case of an if-otherwise statement.
⟨while⟩ → “While” ⟨space⟩ ⟨expression⟩ ⟨comma⟩;
The block of a while statement is continuously executed while its condition evaluates to true.
⟨return⟩ → “Return” (⟨space⟩ ⟨expression⟩)? ⟨period⟩;
Return statements halt the execution of an algorithm, evaluate the expression passed, and pass it up to the algorithm caller. The algorithm call expression will then evaluate to the value returned.
An algorithm must have a return statement at the end of all branches. Either
⟨expression⟩ → ⟨operation⟩ | ⟨algorithm call⟩ | ⟨value⟩ | ⟨variable⟩;
Expressions are used to represent values.
A value can be created as an expression by rendering its literal; see the ⟨integer⟩ and ⟨boolean⟩ rules.
The value a variable contains can later be retrieved with a variable expression that contains its name; see the ⟨variable⟩ rule.
⟨operation⟩ → ⟨unary operation⟩ | ⟨binary operation⟩;
⟨unary operation⟩ → ⟨negation⟩ | ⟨not⟩;
⟨binary operation⟩ → ⟨addition⟩ | ⟨subtraction⟩ | ⟨multiplication⟩ | ⟨division⟩ | ⟨modulo⟩ | ⟨and⟩ | ⟨or⟩ | ⟨greater than or equal to⟩ | ⟨greater than⟩ | ⟨less than or equal to⟩ | ⟨less than⟩ | ⟨equality⟩;
Operations enable the manipulation of the standard data types. Binary operators, like addition, take two expressions, while unary operators take one.
Operators in Gorr are evaluated from left to right; there is no operator precedence.
⟨negation⟩ → “the negation of” ⟨space⟩ ⟨expression⟩;
⟨addition⟩ → “the addition of” ⟨space⟩ ⟨expression⟩ ⟨space⟩ “and” ⟨space⟩ ⟨expression⟩;
⟨subtraction⟩ → “the subtraction of” ⟨space⟩ ⟨expression⟩ ⟨space⟩ “from” ⟨space⟩ ⟨expression⟩;
⟨multiplication⟩ → “the multiplication of” ⟨space⟩ ⟨expression⟩ ⟨space⟩ “by” ⟨space⟩ ⟨expression⟩;
⟨multiplication⟩ → “the division of” ⟨space⟩ ⟨expression⟩ ⟨space⟩ “by” ⟨space⟩ ⟨expression⟩;
⟨modulo⟩ → “the modulo of” ⟨space⟩ ⟨expression⟩ ⟨space⟩ “by” ⟨space⟩ ⟨expression⟩;
These operators implement the standard arithmetic operators; they take in integers and evaluate to integers. Because Gorr only has integers, when dividing, the remainder is disposed of; it can be retrieved with the modulo.
⟨not⟩ → “not” ⟨space⟩ ⟨expression⟩;
⟨and⟩ → “both” ⟨space⟩ ⟨expression⟩ ⟨space⟩ “and” ⟨expression⟩;
⟨or⟩ → “either” ⟨space⟩ ⟨expression⟩ ⟨space⟩ “or” ⟨expression⟩;
These operators implement the standard Boolean operators; they take in Booleans and evaluate to Booleans.
⟨equality⟩ → ⟨expression⟩ ⟨space⟩ “is equal to” ⟨space⟩ ⟨expression⟩;
⟨greater than or equal to⟩ → ⟨expression⟩ ⟨space⟩ “is greater than or equal to” ⟨space⟩ ⟨expression⟩;
⟨greater than⟩ → ⟨expression⟩ ⟨space⟩ “is greater than” ⟨space⟩ ⟨expression⟩;
⟨less than or equal to⟩ → ⟨expression⟩ ⟨space⟩ “is less than or equal to” ⟨space⟩ ⟨expression⟩;
⟨less than⟩ → ⟨expression⟩ ⟨space⟩ “is less than” ⟨space⟩ ⟨expression⟩;
The equivalence operator evaluates to true if both expressions evaluate to the same value.
Both expressions must be the same type.
The inequality operators work as one would expect: they take in integers and evaluate to booleans.
⟨algorithm call⟩ → “call” ⟨space⟩ ⟨variable⟩ (“arguments” ⟨space⟩ ⟨expression⟩ (⟨comma⟩ ⟨space⟩ ⟨expression⟩)*)?;
This expression takes the name of an algorithm along with a list of specified arguments, runs the algorithm with said arguments, and evaluates to its return value.
The algorithm [[ factorial ]], with the signature integer [[a]] returns integer, does the following:
1. If either [[a]] is equal to 0 or [[a]] is equal to 1,
1.1. Return 1.
2. Otherwise,
2.1. Return the multiplication of [[a]] by call [[factorial]] arguments the subtraction of 1 from [[a]].
The algorithm [[ absolute value ]] with the signature integer [[ a ]] returns integer, does the following:
1. If [[ a ]] is greater than or equal to 0,
1.1. Return [[ a ]].
2. Otherwise,
2.1. Return the negation of [[ a ]].
The algorithm [[ greatest common denominator ]] with the signature integer [[ u ]], integer [[ v ]] returns integer, does the following:
1. While [[ v ]] is greater than 0,
1.1. The integer [[ previous u ]] is [[ u ]].
1.2. Set [[ u ]] to [[ v ]].
1.3. Set [[ v ]] to the modulo of [[ previous u ]] by [[ v ]].
2. Return call [[ absolute value ]] arguments [[ u ]].
The algorithm [[ least common multiple ]] with the signature integer [[ u ]], integer [[ v ]] returns integer, does the following:
1. If both [[ u ]] is greater than 0 and [[ a ]] is greater than 0,
1.1. Return the division of call [[ absolute value ]] arguments the multiplication of [[ a ]] by [[ b ]] by call [[ greatest common denominator ]] arguments [[ u ]], [[ v ]].
2. Otherwise,
2.1. Return 0.
[1] In this specification, data type will usually be shortened to just type.